3 Creative Ways to Visualize Outliers in Tableau

There are many ways to detect outliers in your data, but flagging them for your end users may present some challenges. Understanding the logic to clearly communicate it to your stakeholders, finding the right method to use, implementing it in a visual format, and the list goes on. To help you overcome these challenges, I am going to walk you through three ways to identify outliers in Tableau and how to visualize each.

By the end of this tutorial, you will be able to use standard deviations, median with quartiles, and Z-scores to flag outliers in your data and present them visually to your stakeholders.

Learn How to Do Anomaly Detection with Playfair+

View / Interact / Download

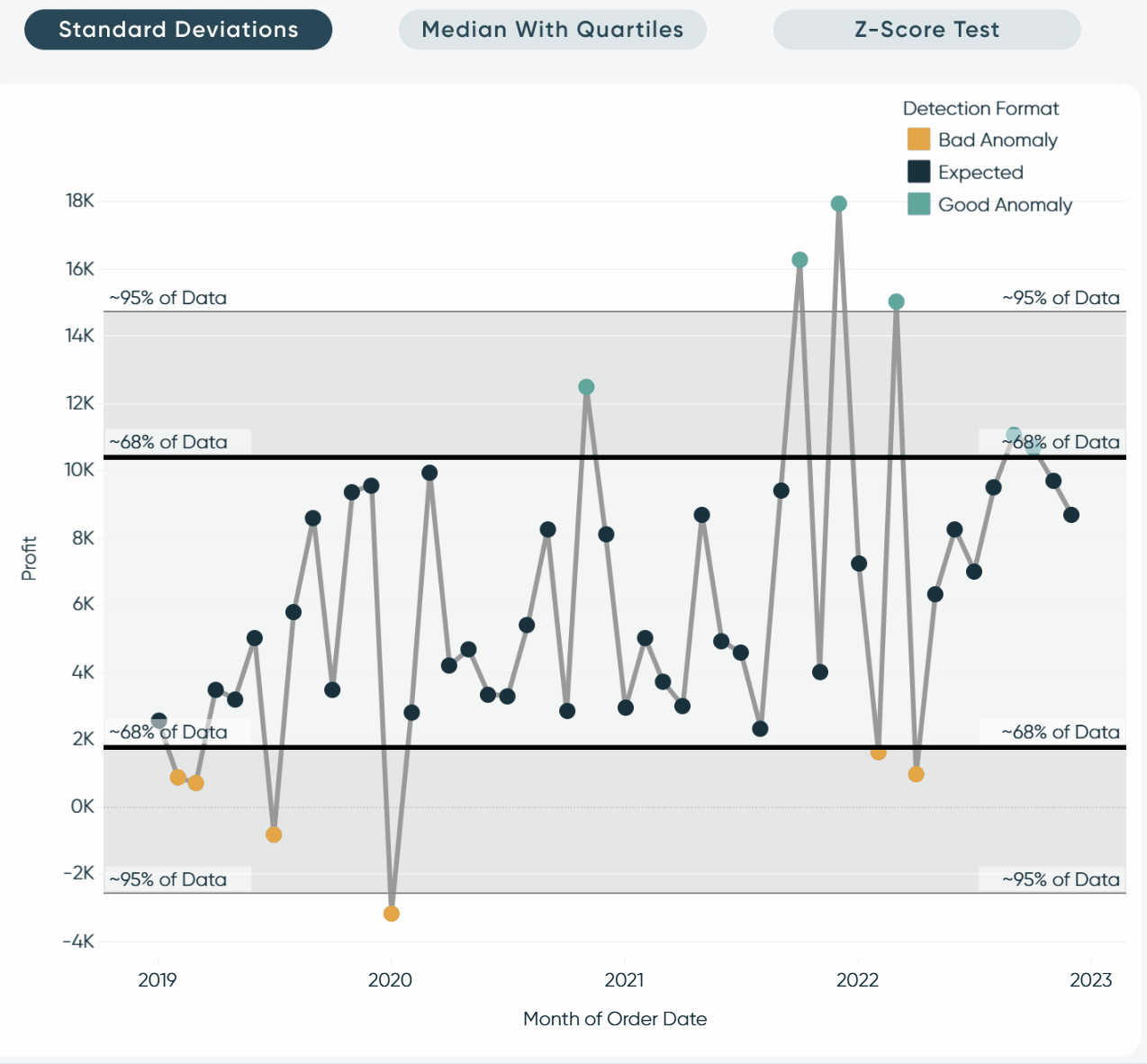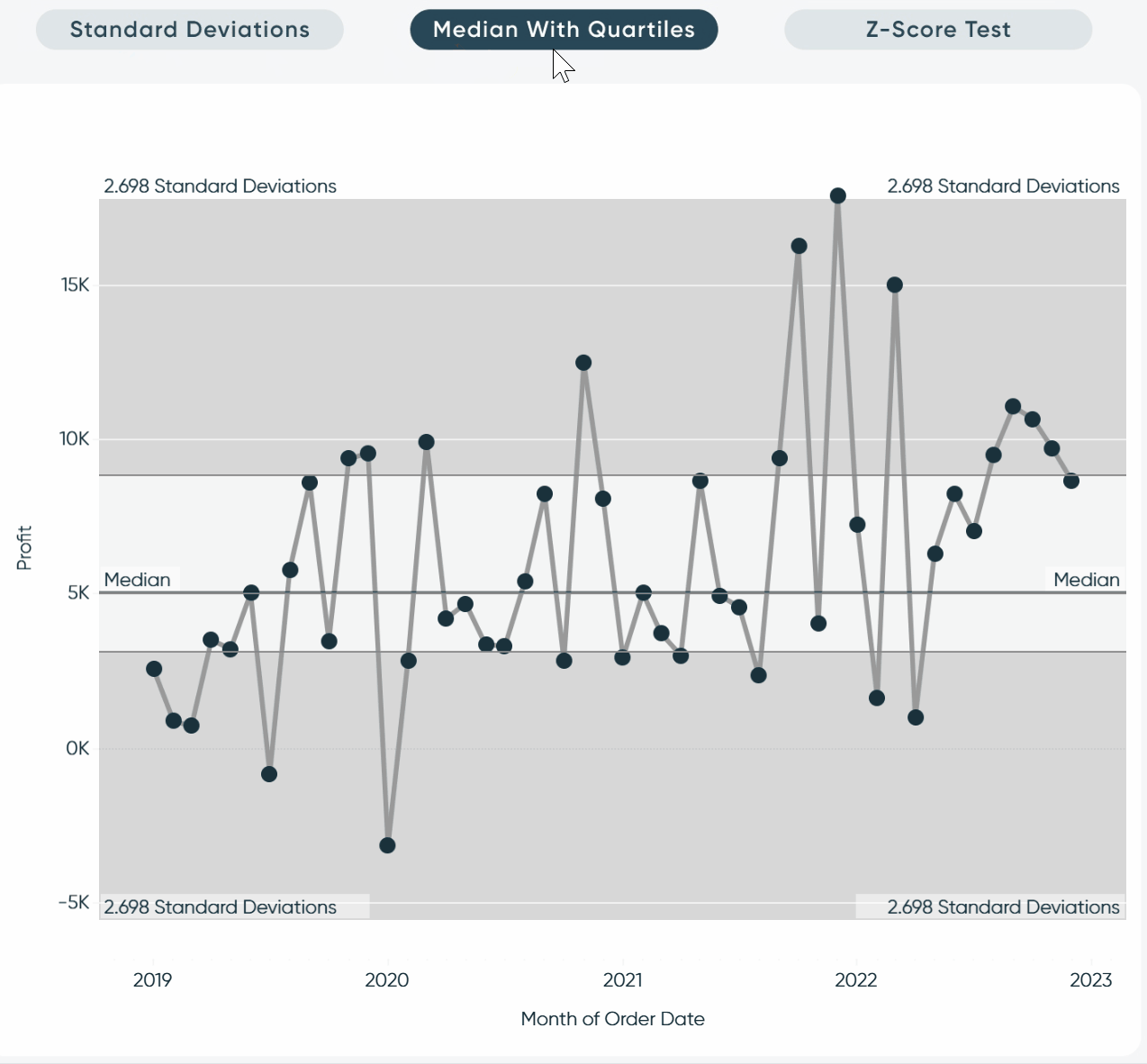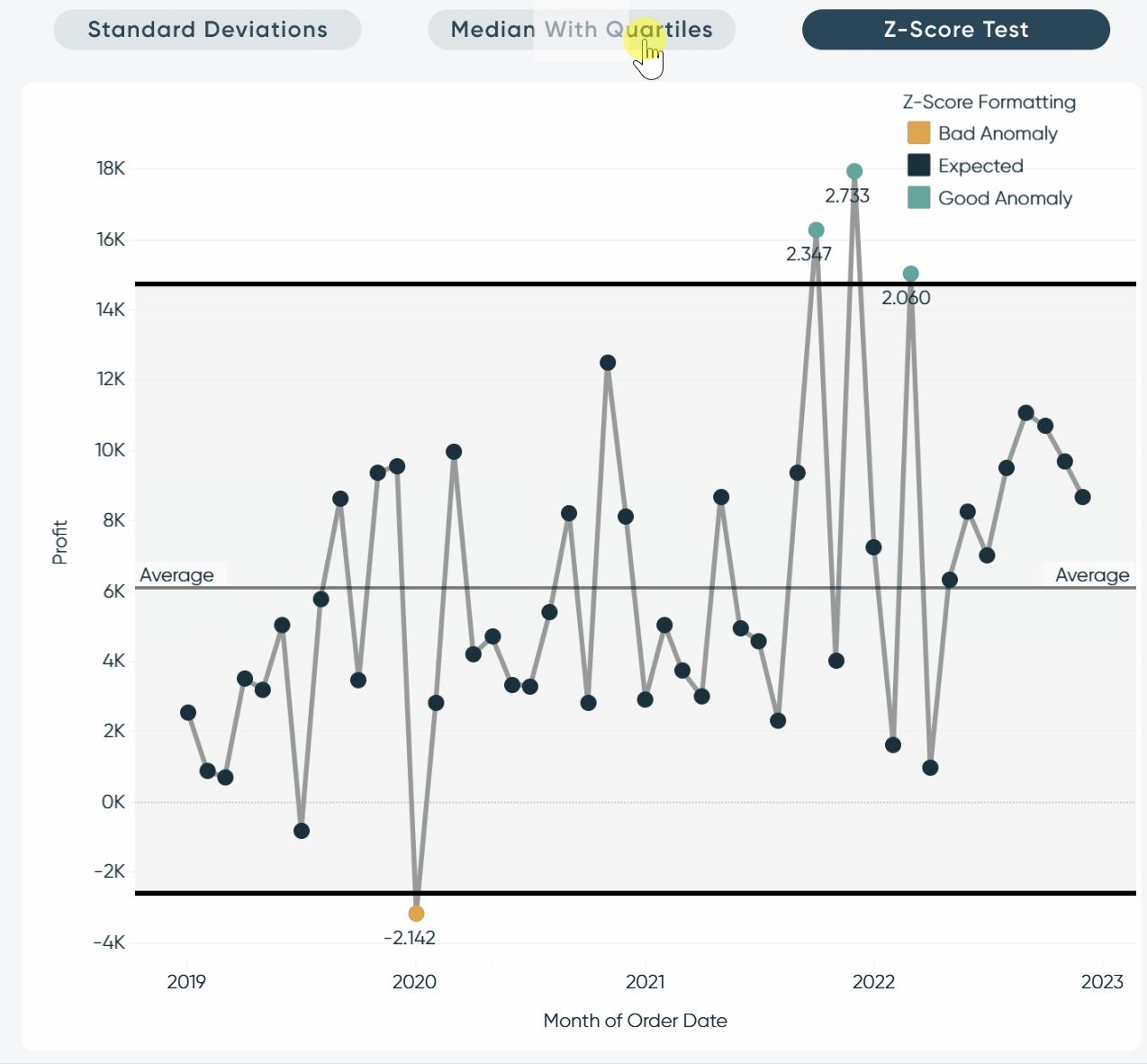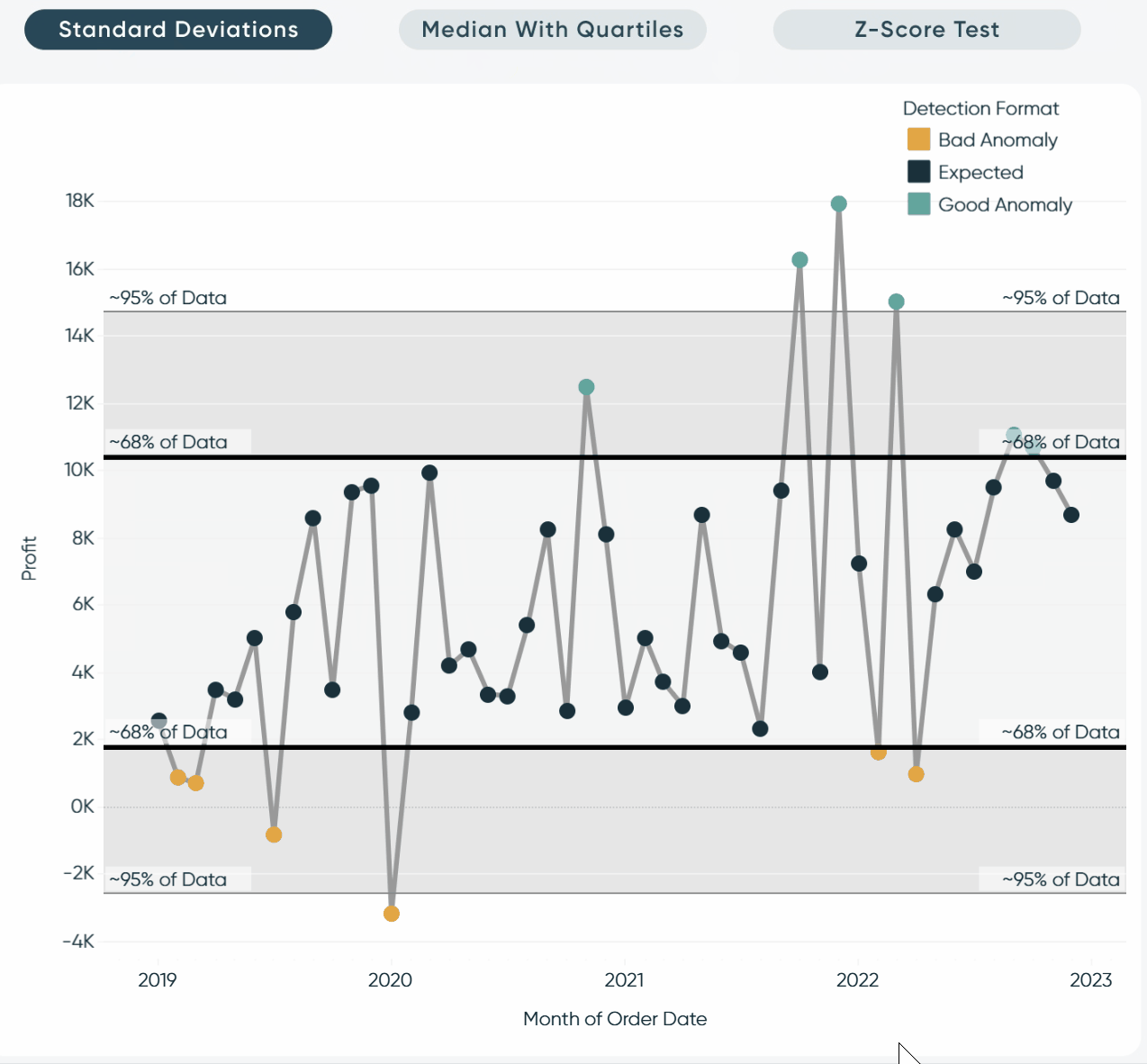
Standard deviations

For this first method, I am going to use standard deviations to identify outliers. To kick us off, I have plotted a dual-axis line chart of the SUM of profit.

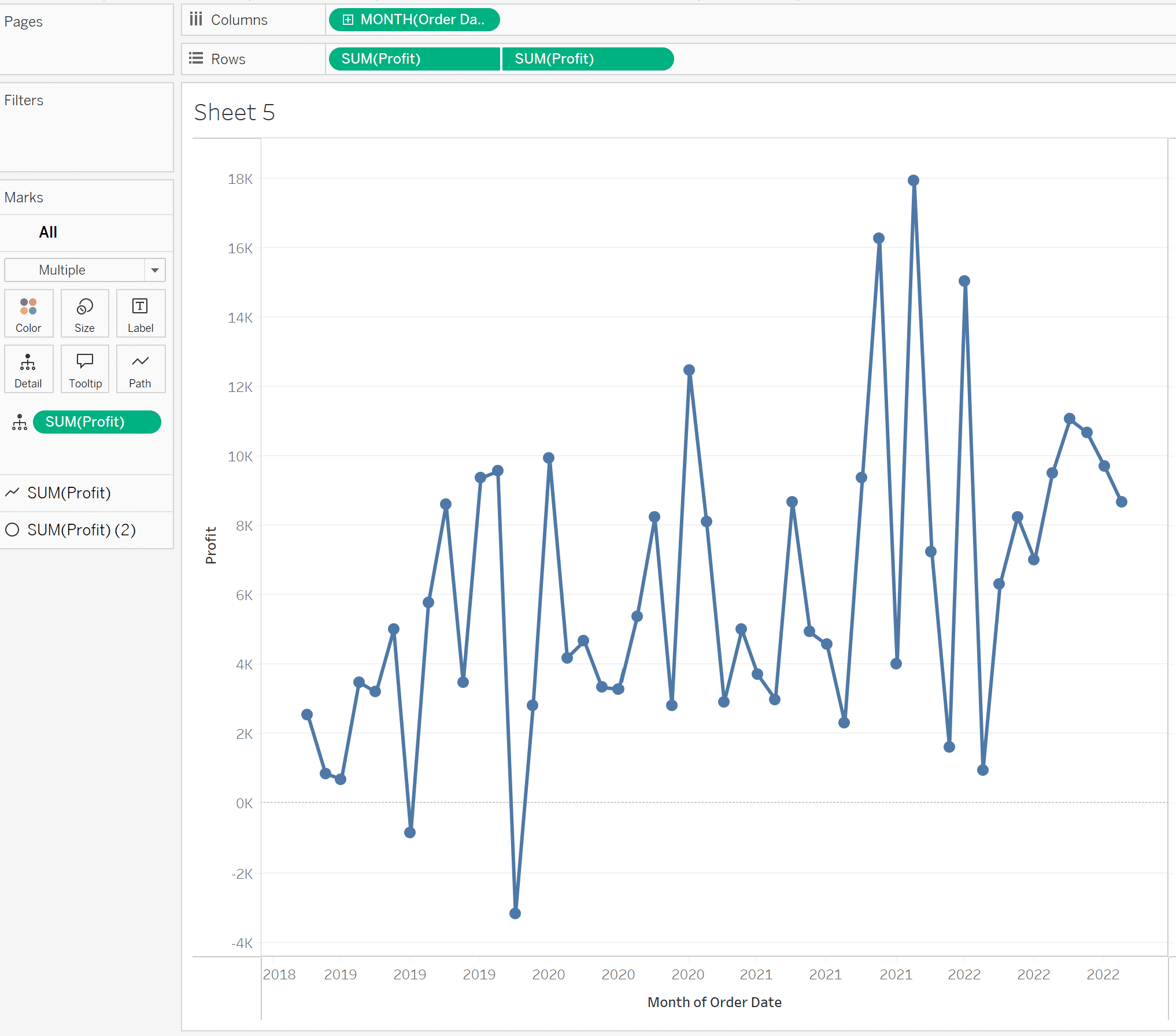
My intention here is to flag everything above 1 standard deviation from the average, which I would consider an anomaly. Then, visually show everything above 2 standard deviations as an outlier.

Join 25K+ leaders using Playfair Data to make better decisions.
 

Δ

Email(Required)

To begin, I will add reference lines that will show +/- 2 standard deviations.

Note: I want to start with the wider distribution band first for formatting purposes, but you could go either way here.

To add that set of reference lines, I will toggle to the Analytics Pane by clicking on that pane in the top left of the authoring interface.

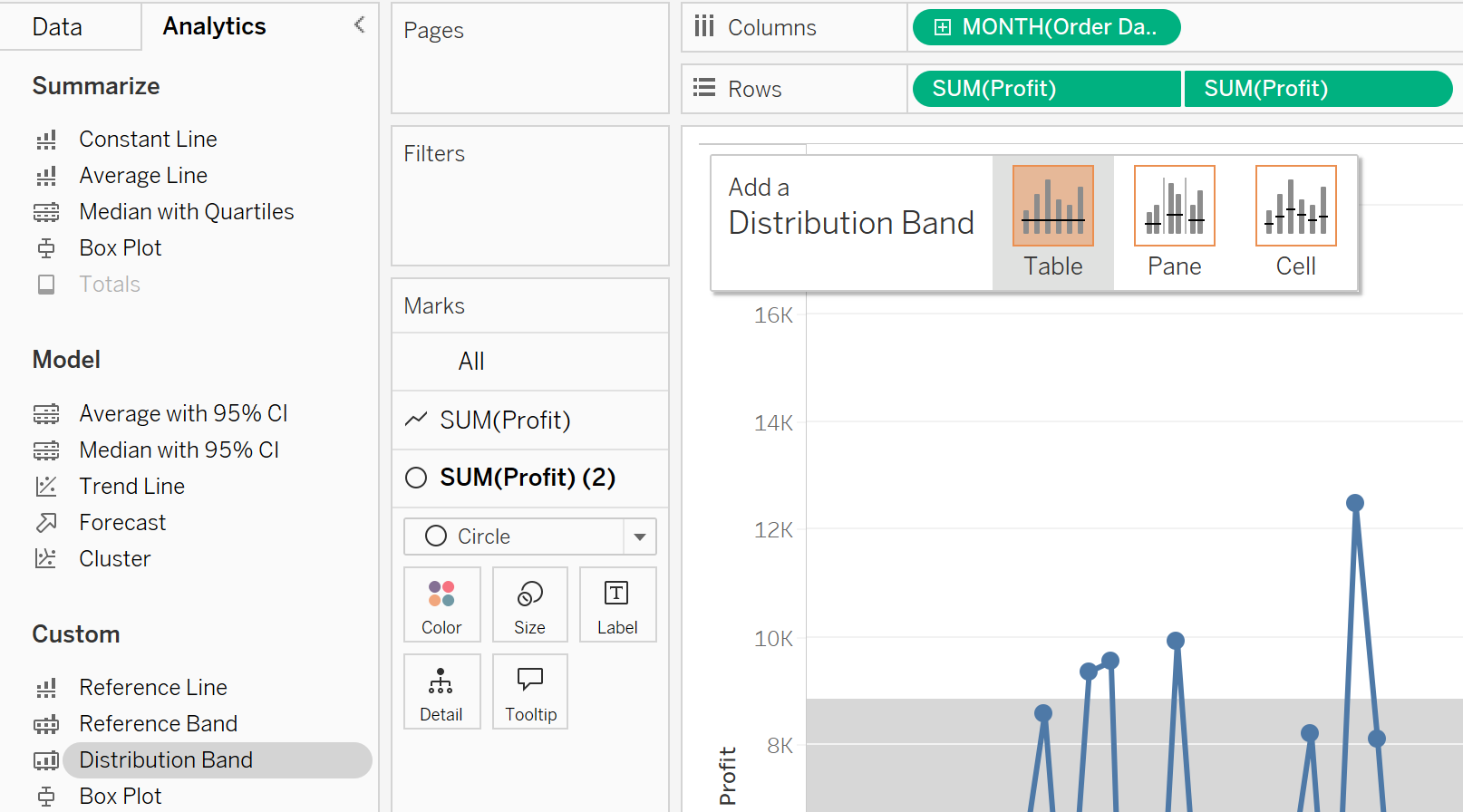
Then I will click and drag Distribution Band onto the view.

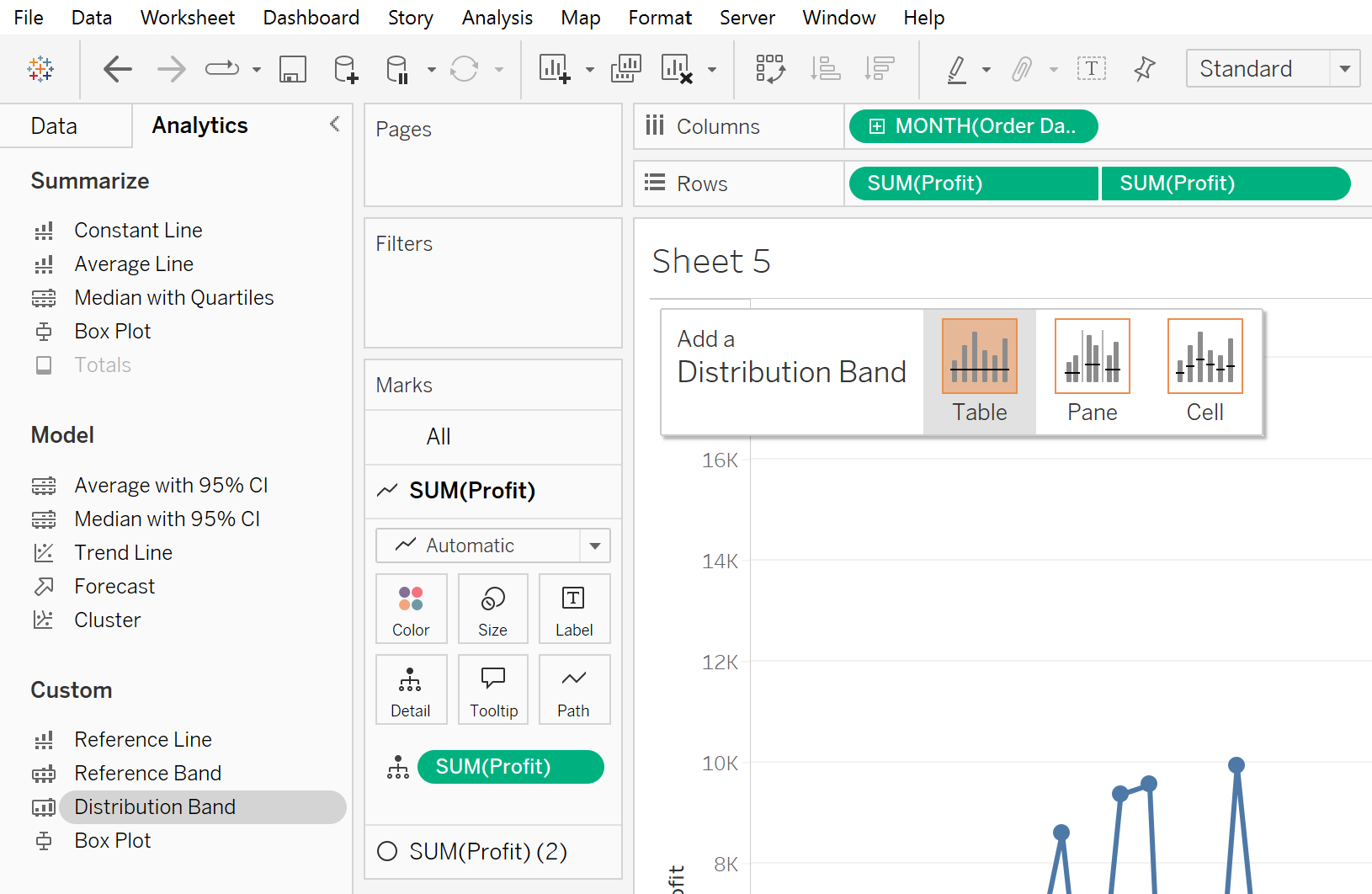
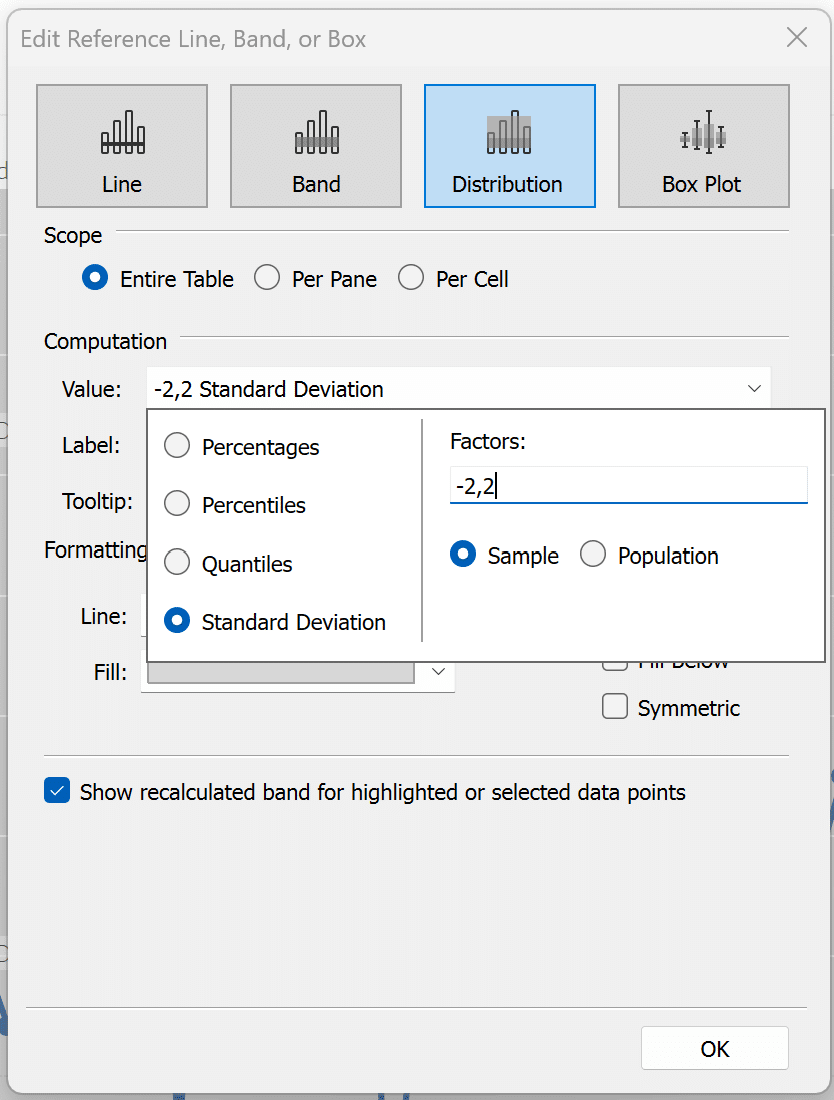
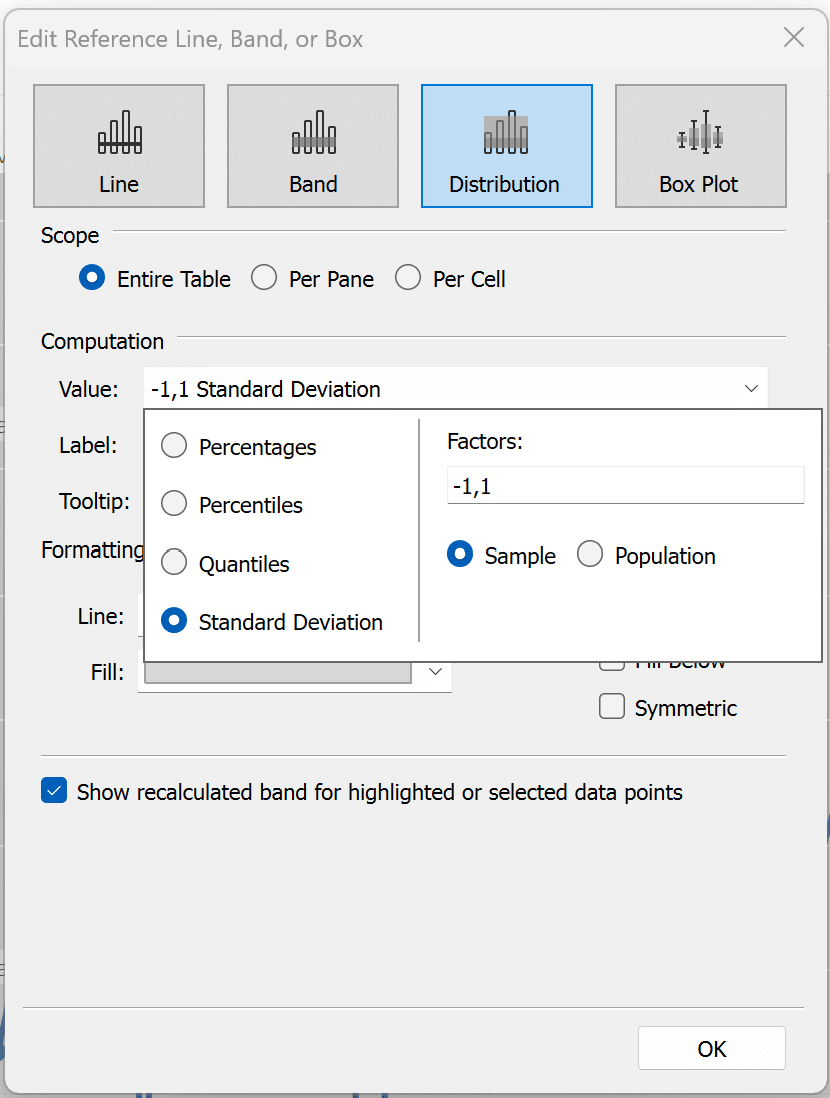
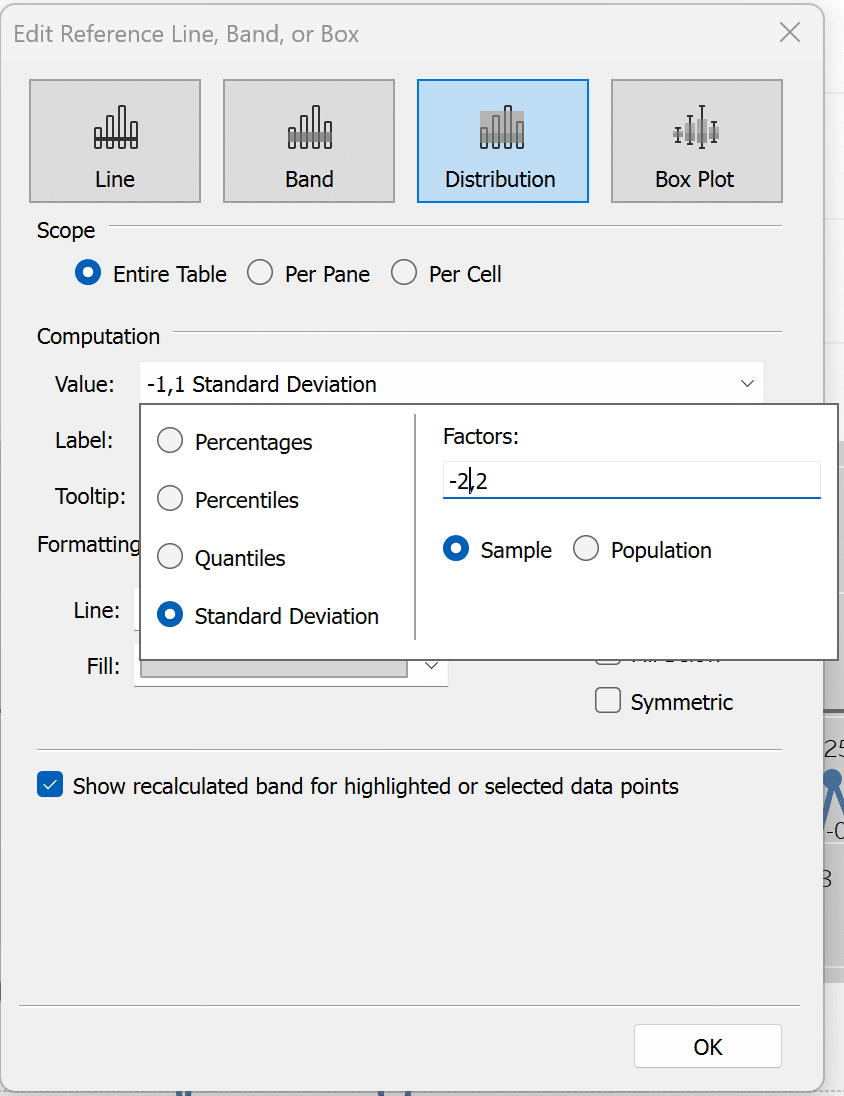
After adding the band to the view, you will be presented with the editing menu. Click the Value dropdown and select the Standard Deviation radio button. Then in the Factors box type “-2,2”. This signifies plus or minus 2 standard deviations. After that click OK to close the menu.

We will now see those bands appear in our view.

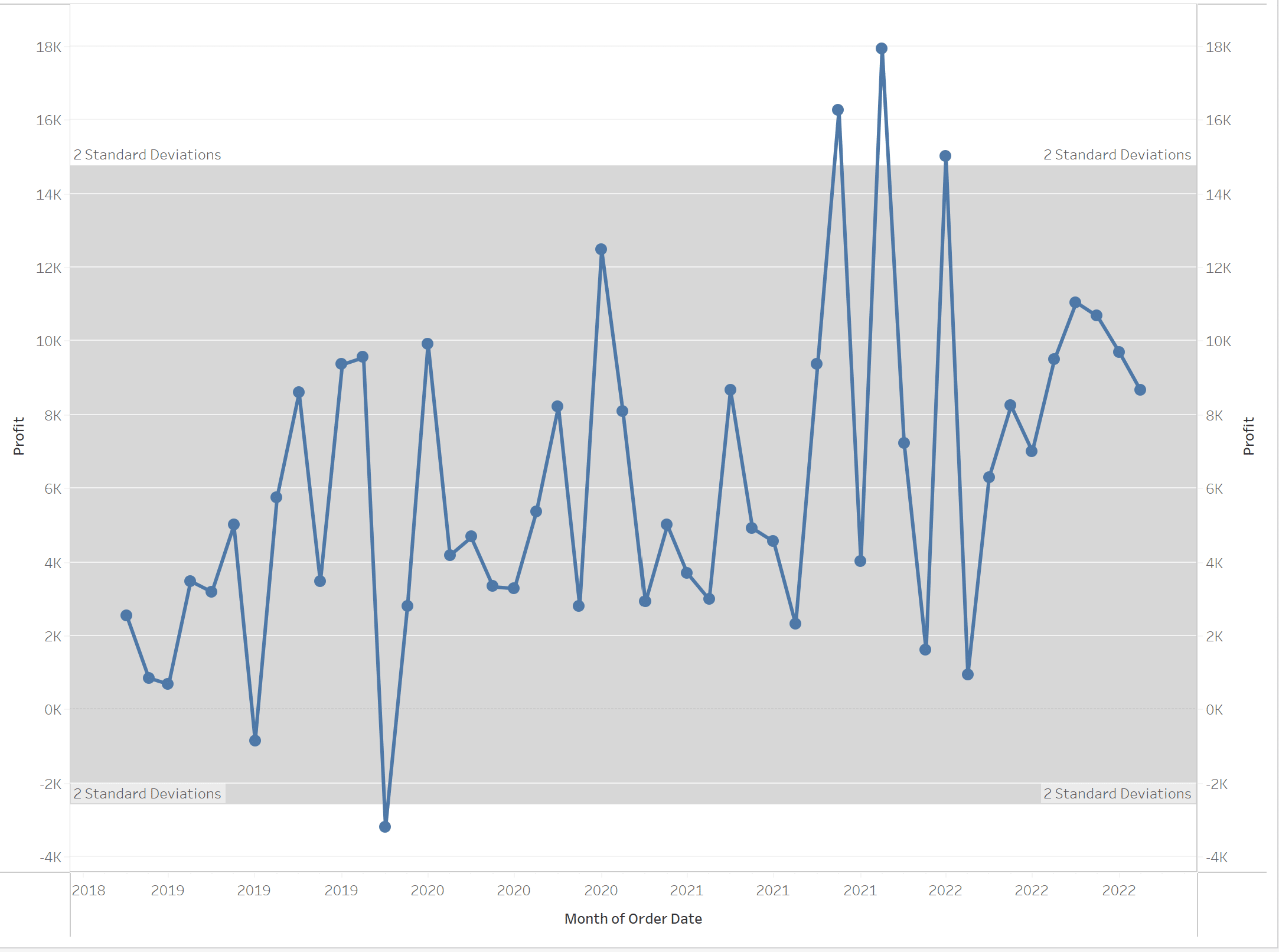
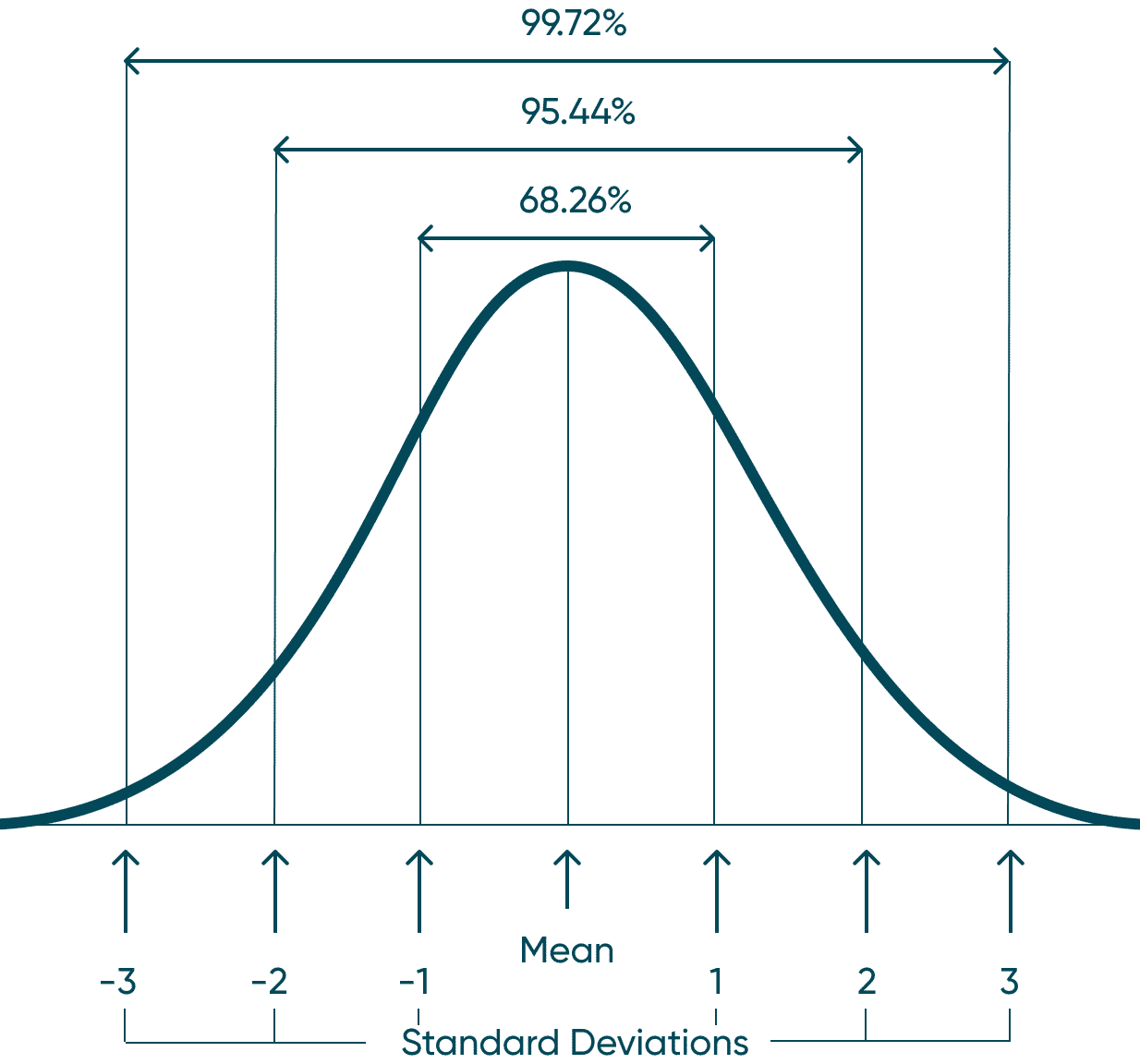
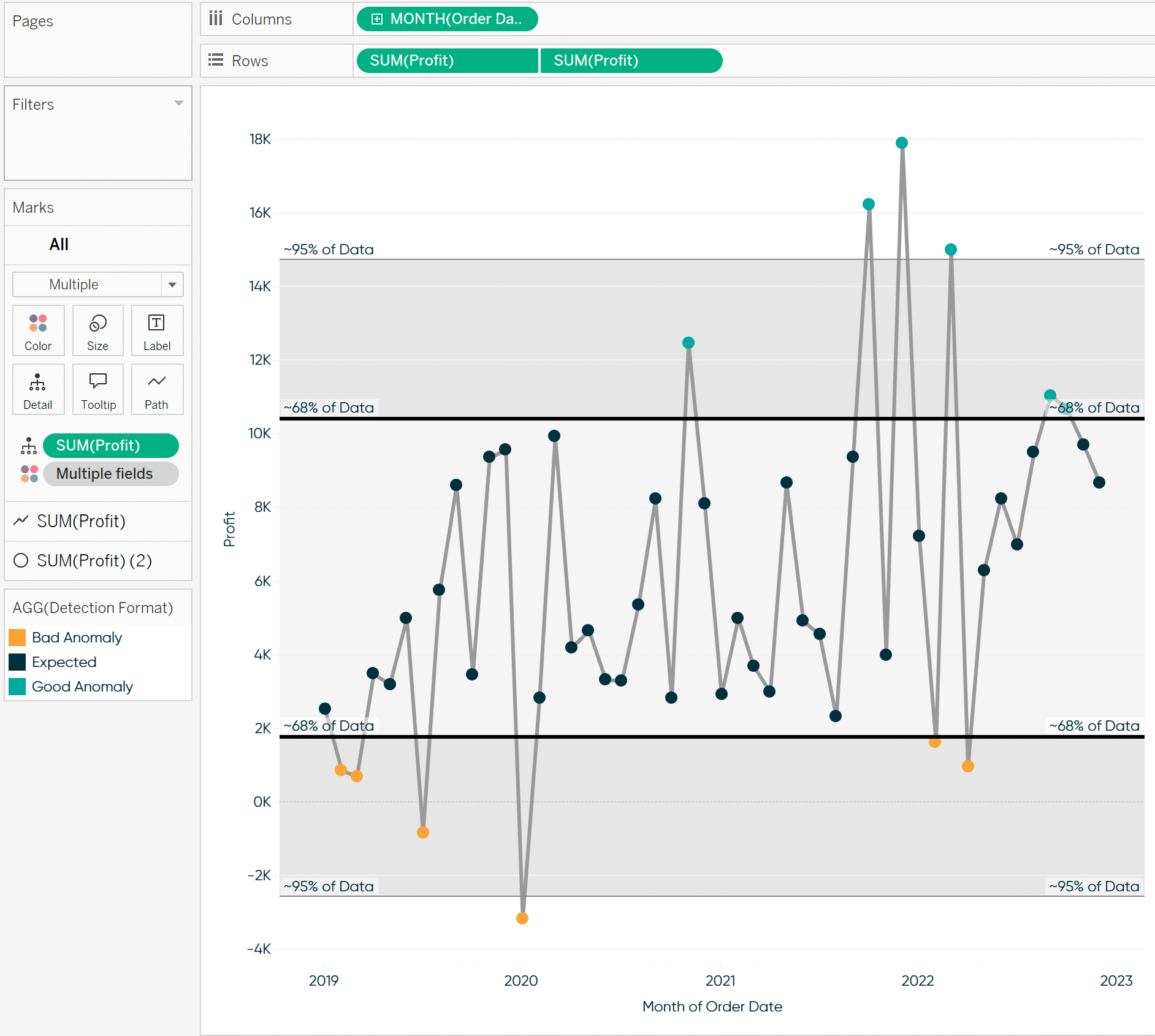
Again, anything above or below these bands I would consider an outlier in your data. Roughly 95% of your data should fall within 2 standard deviations, as seen in the helpful graphic below.

Next, I want to add another set of reference lines to signify plus or minus 1 standard deviation. This is not required, but I think it cleans up the view and gives your end users more context. I will repeat the steps I completed above, but I will leave the “-1,1” in the factors section of the menu.

Last, I am going to clean up the view a little and add conditional formatting on the marks in my view. Use this calculation below for the same formatting.

IF SUM([Profit]) <  (WINDOW_AVG(SUM([Profit])) – WINDOW_STDEV(SUM([Profit]))) THEN ‘Bad Anomaly’
ELSEIF SUM([Profit]) > (WINDOW_AVG(SUM([Profit])) + WINDOW_STDEV(SUM([Profit]))) THEN ‘Good Anomaly’
ELSE ‘Expected’
END

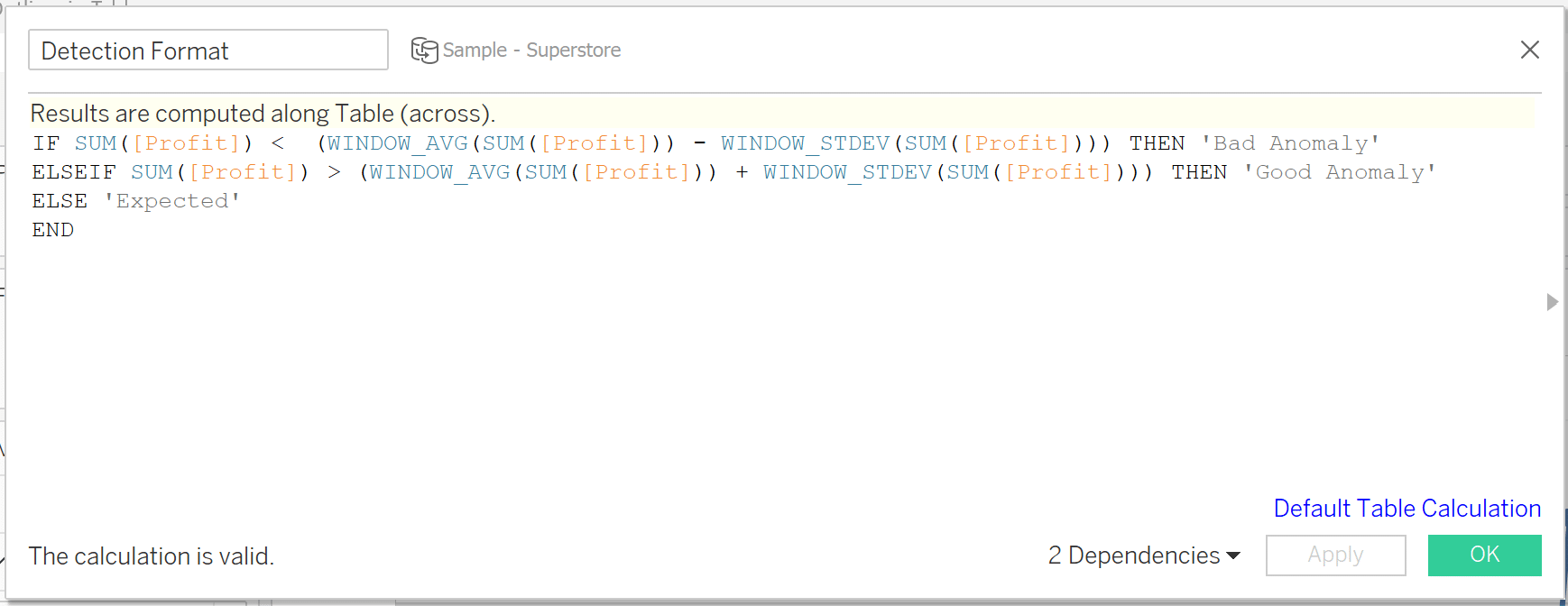
In this calculation, I am basically flagging anything +/- 1 standard deviation and marking it as an anomaly. After formatting, I landed on the following view.

Median with quartiles

For this method to visualize outliers, I am basically creating a box-and-whisker plot manually using reference lines. However, while you would get the same data points by applying a box-and-whisker plot, it limits our formatting options.  It is also far less intimidating to your stakeholders to see it displayed with clear reference bands when compared to the box-and-whisker. At the end, I will display both side-by-side so you can see the difference that building it out yourself has on the overall UX.

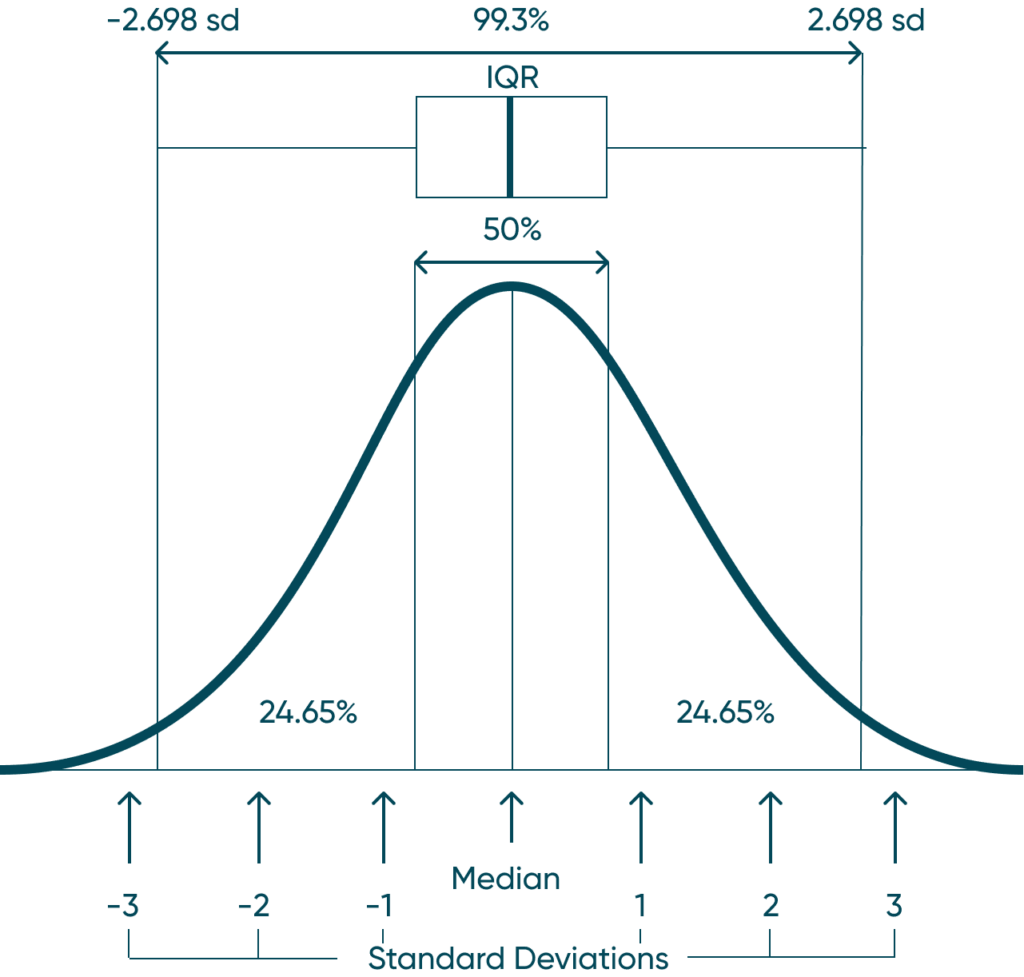
To get a feel for the end result, I have created a graphic that you can reference to explain how we are flagging outliers. First, we are going to add a median line with quartiles. This will show us the Median as well as the upper and lower bounds. This band will represent about 50% of your observable data. This 50% band is called an interquartile range – also known as IQR – and would make up the “box” of a traditional box-and-whisker plot. Next, we will be adding a reference band of +/- 2.698 standard deviations. This is going to give us roughly the upper and lower whiskers. The one drawback of this implementation is a box-and-whisker plot will place the bounds directly on the min and max value within the whisker. Check out the side-by-side comparison to get a sense for what I am talking about.

To start, I am going to use the same dual-axis line chart as before.

I’ll toggle to the Analytics pane again and drag Median with Quartiles onto the view.

This will display our median and our interquartile range on the view.

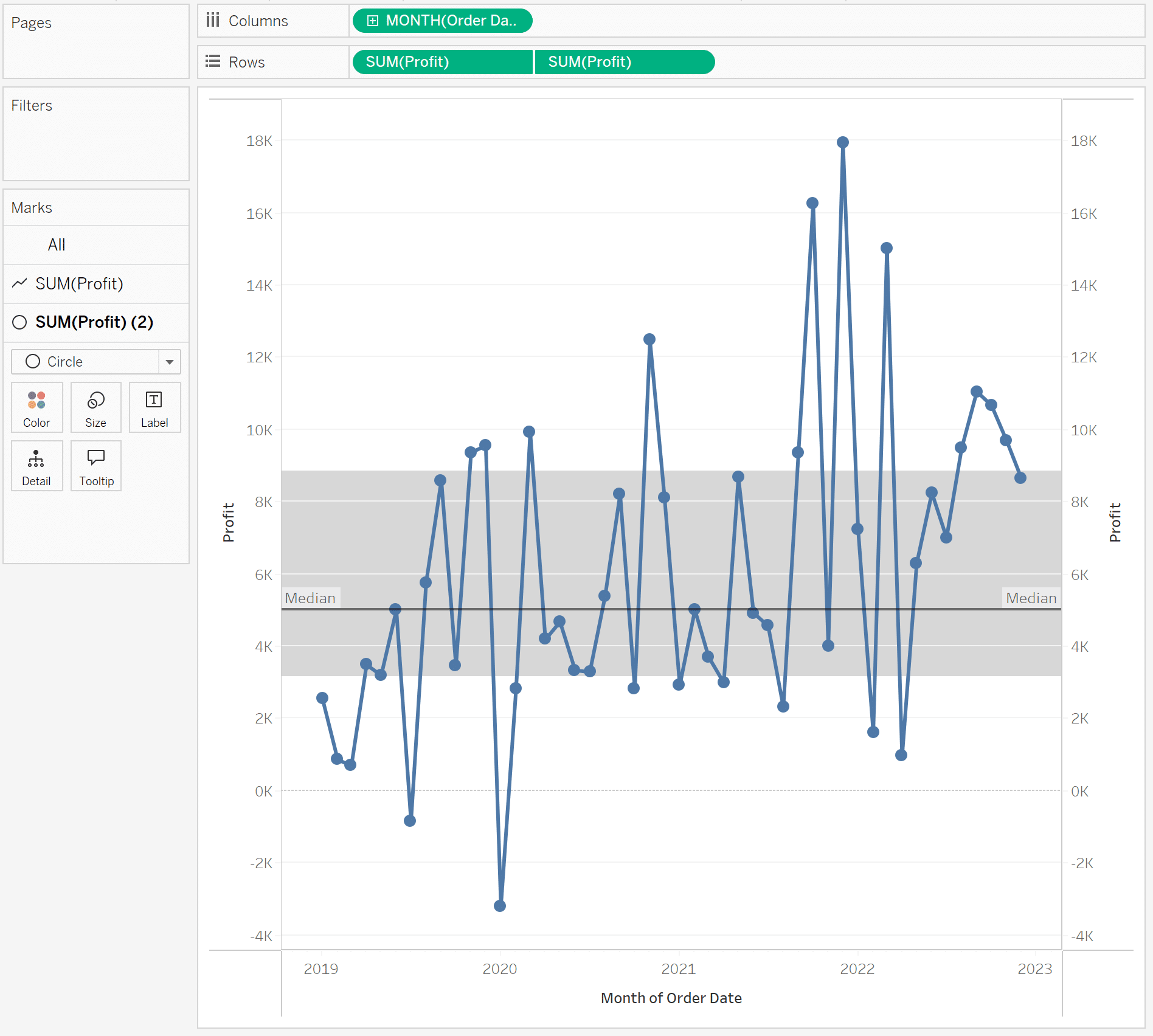
In a traditional box-and-whisker plot, this would be the “box.” Basically, about 50% of our data would fall in this range. We are missing the “whisker” which would represent our upper and lower bounds and would show us what would be considered outliers using this method.

To add the “whisker,” I will drag Distribution Band from the Analytics pane onto my view.

In the menu that pops up, I will click on the Value dropdown, select Standard Deviation, and enter “-2.698,2.698” into the Factors text box.

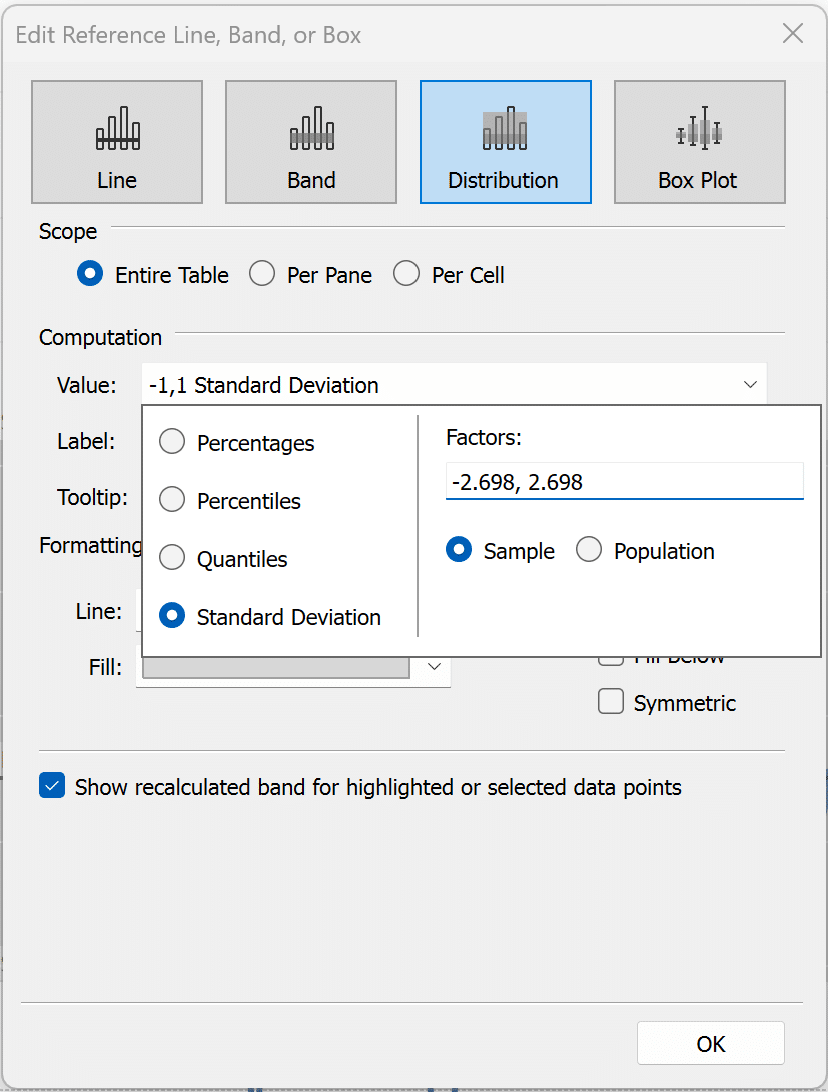
Then I will click OK to close the menu and format it similarly to the last section.

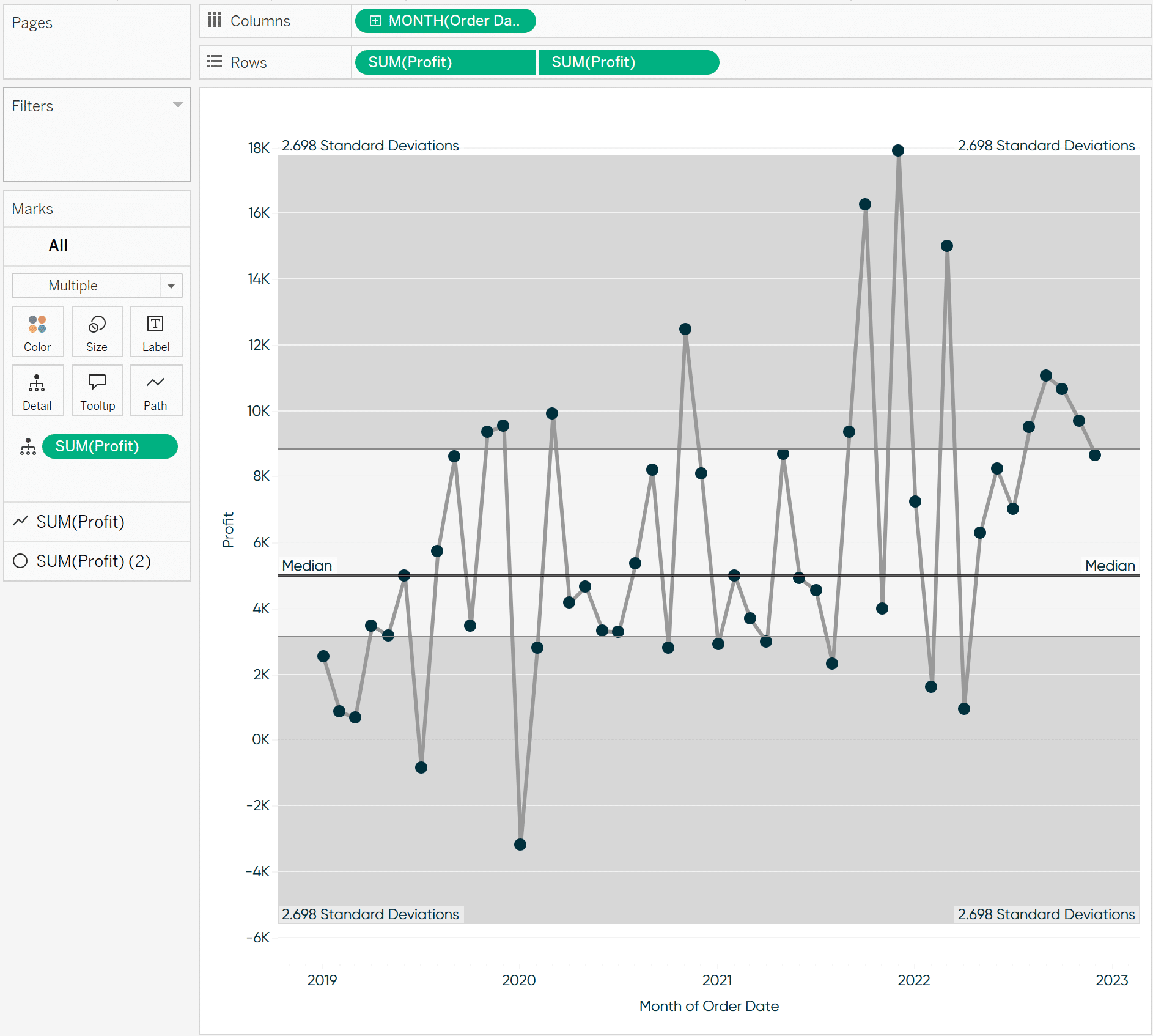
We can see only one mark on the view fell above our upper bounds. Compare that to our traditional box-and-whisker plot below.

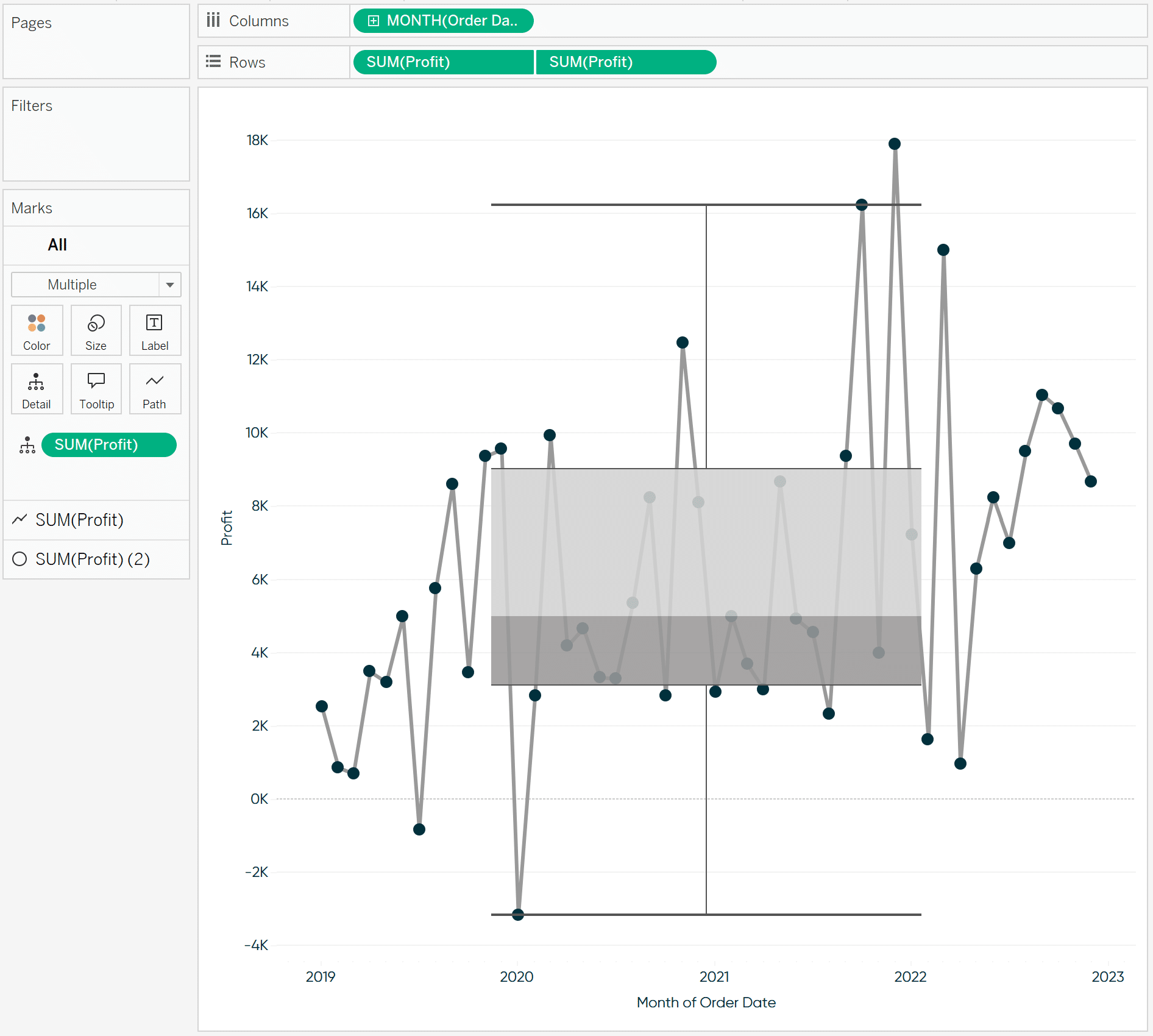
While we do get the same data points, the view is pretty poorly laid out and could raise more questions than answers.

Z-score testing

For the final method to visualize outliers, I will show you how to implement Z-scores. Calculating out a Z-score is a great way to index the marks in your view and gives you a simple way to explain outliers to your stakeholders. To calculate a Z-score, take the value of the mark, subtract the average, and then divide by the standard deviation. The mathematical formula is:

z = (x – μ) / σ
standard score = observed value – mean of sample / standard deviation of the sample

This formula will return how many standard deviations above or below that mark is from the mean. For instance, if the Z-score of a mark is two that means that mark is two standard deviations from the average. If a Z-score is zero that means the mark equals the average.

Create a free account, or login.

Unlock this tutorial and hundreds of other free visual analytics resources from our expert team.

Already have an account? Sign In

Δ

Phone

This field is for validation purposes and should be left unchanged.

Name

First Last

Email

Password

Enter Password Confirm Password

By continuing, you agree to our Terms of Use and Privacy Policy.

or

---

Continue with Google

Continue with LinkedIn

Explore unlimited access to all offerings. See membership options.

A few final things to note about Z-scores. You need to have a decent sample size to get accurate results using this method. My rule of thumb is at least 30 marks in the view to get a decent sample size. However, this depends on your data. The best practice is to see if your data follows a normal distribution by plotting a histogram. For more on that check out the related content below.

Using Median Absolute Deviation in Tableau to Detect Outliers 

Last caveat; it’s standard to consider any Z-score +/- 3 as an outlier but, as I mentioned in the other sections, this is up to interpretation and pretty arbitrary depending on how accurate you want to be. For this demonstration, I will flag anything +/- 2 as an outlier.

Learn to navigate uncharted waters.

Upgrade to Core or Premium benefits to take your data skills even further.

Upgrade now

To calculate a Z-score in Tableau, we will use the following formula:

(SUM([Profit]) – WINDOW_AVG(SUM([Profit]))) / WINDOW_STDEV(SUM([Profit]))

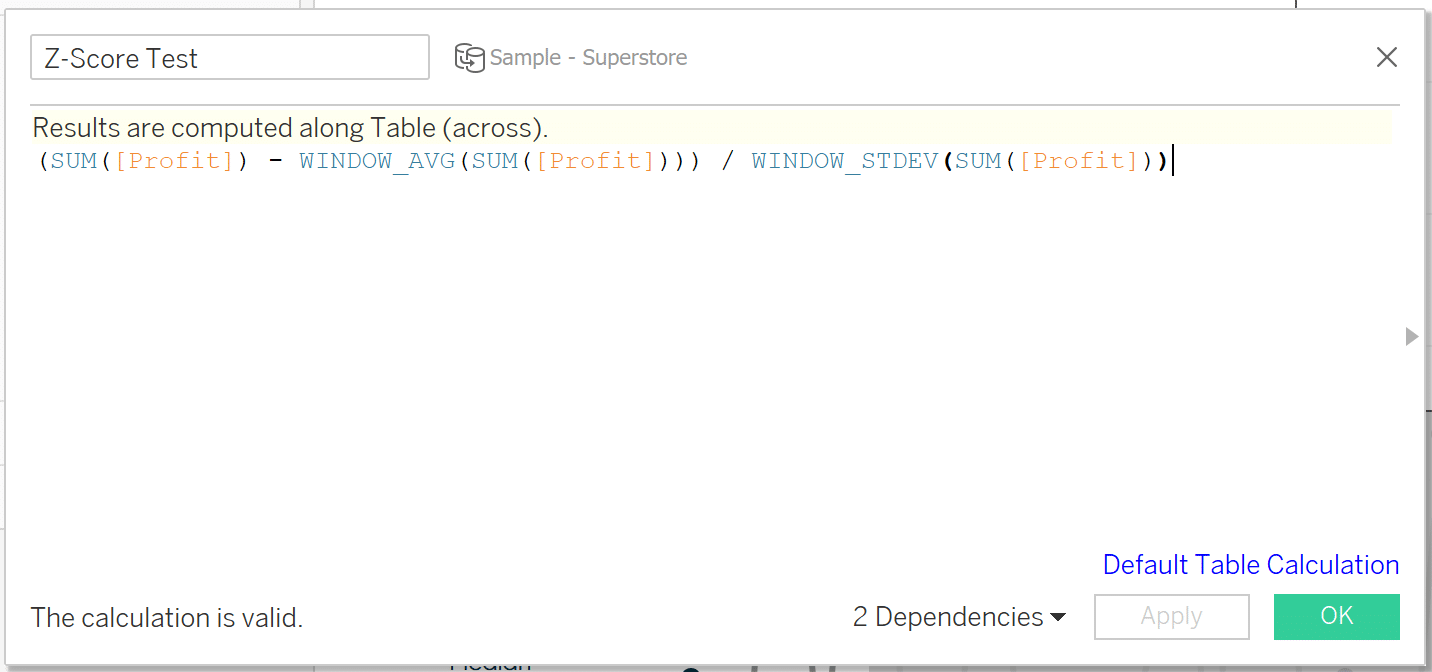
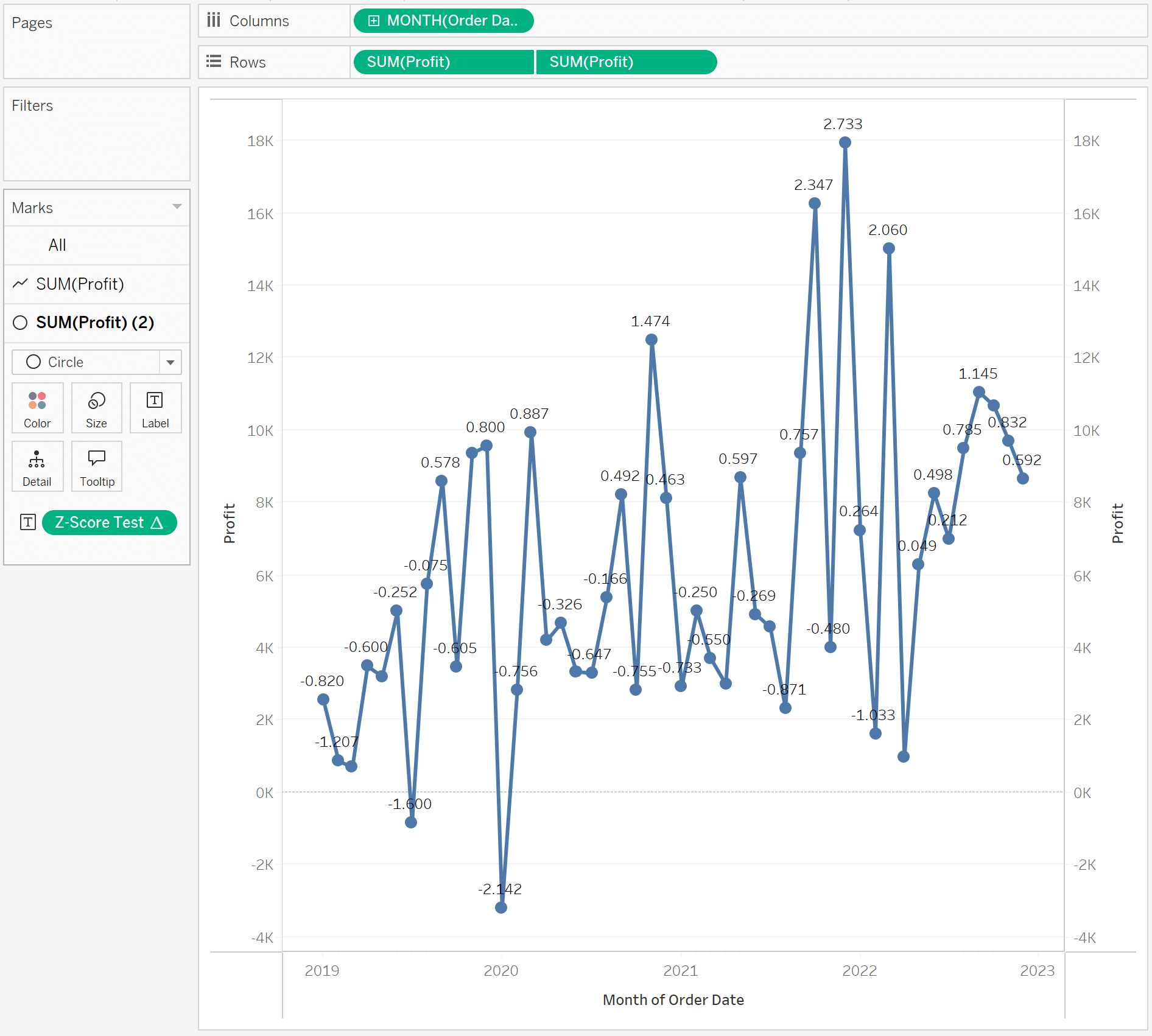
To see this method in action, I will add it to the Text property of my Marks card using the same dual-axis line chart from the other examples.

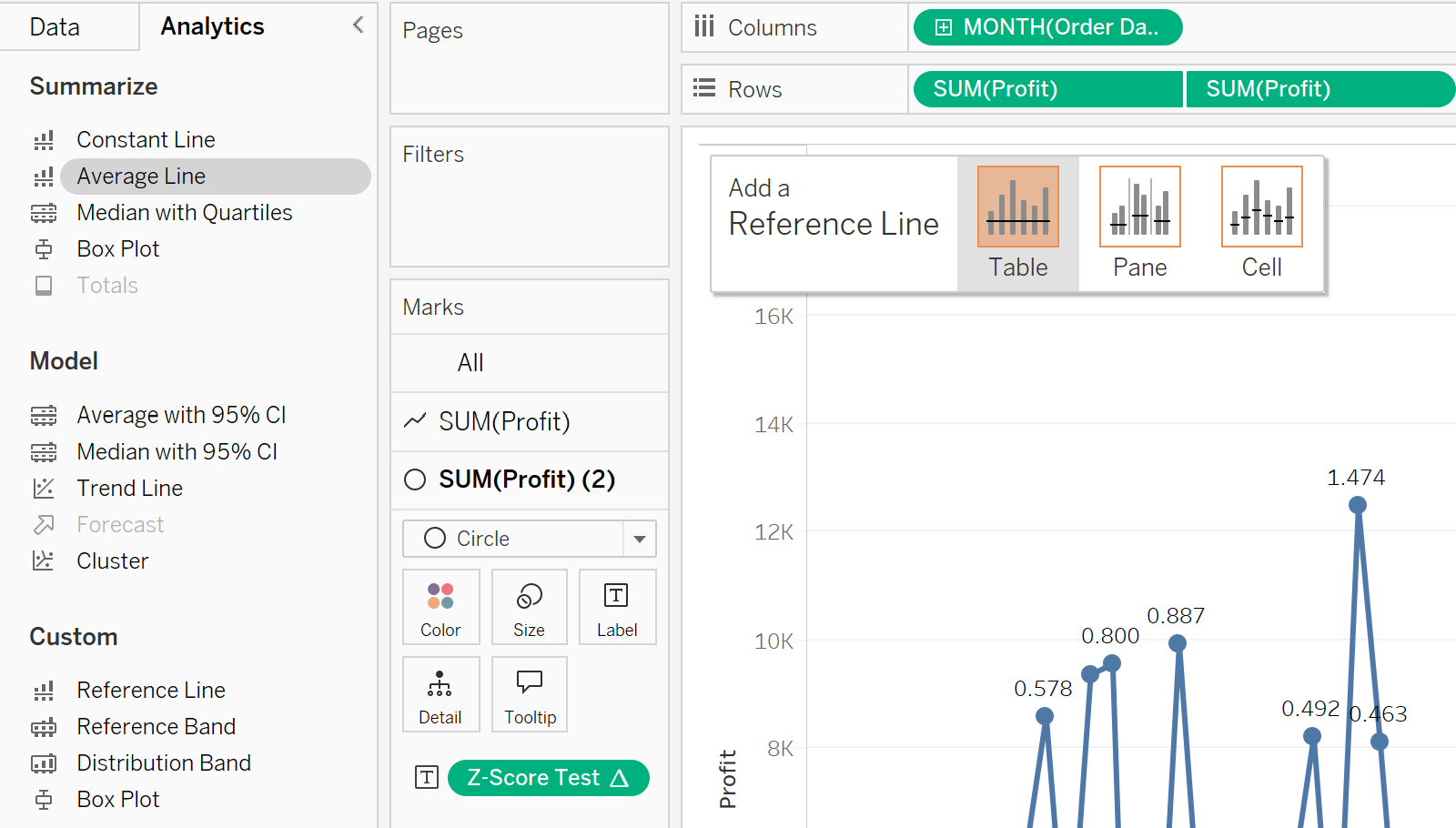
To give users context, I will add an average line by toggling to the Analytics pane and dragging Average Line to the view.

You can see that the positive and negative Z-scores oscillate around that line.  This is a good pressure test for the formula.

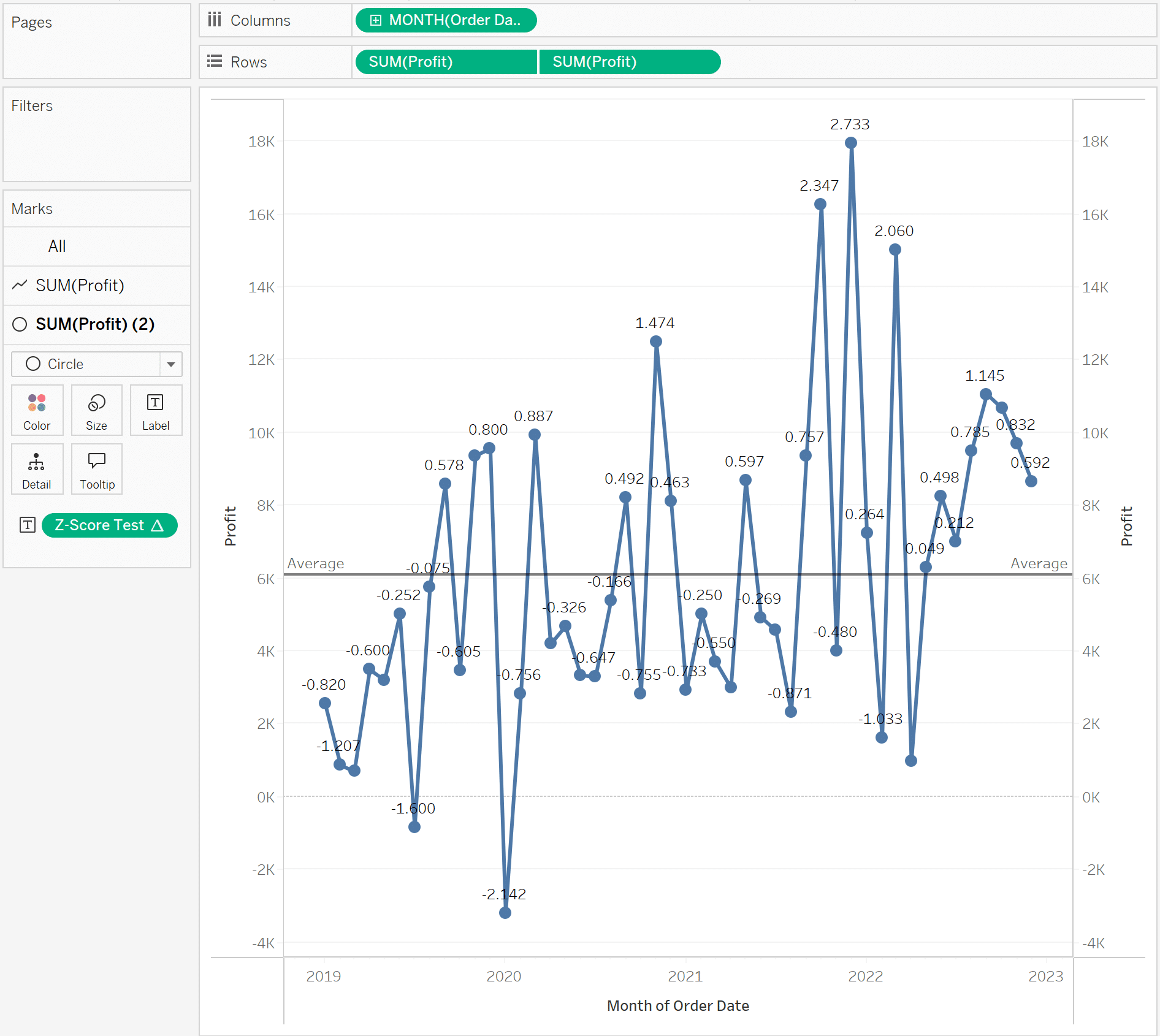
Next, I want to add some more reference lines to indicate what is outside of the +/- 2 range. To do this, I will drag Distribution Band onto the view. In the menu, I will click the Value dropdown, select Standard Deviation, and change the Factors to “-2,2”

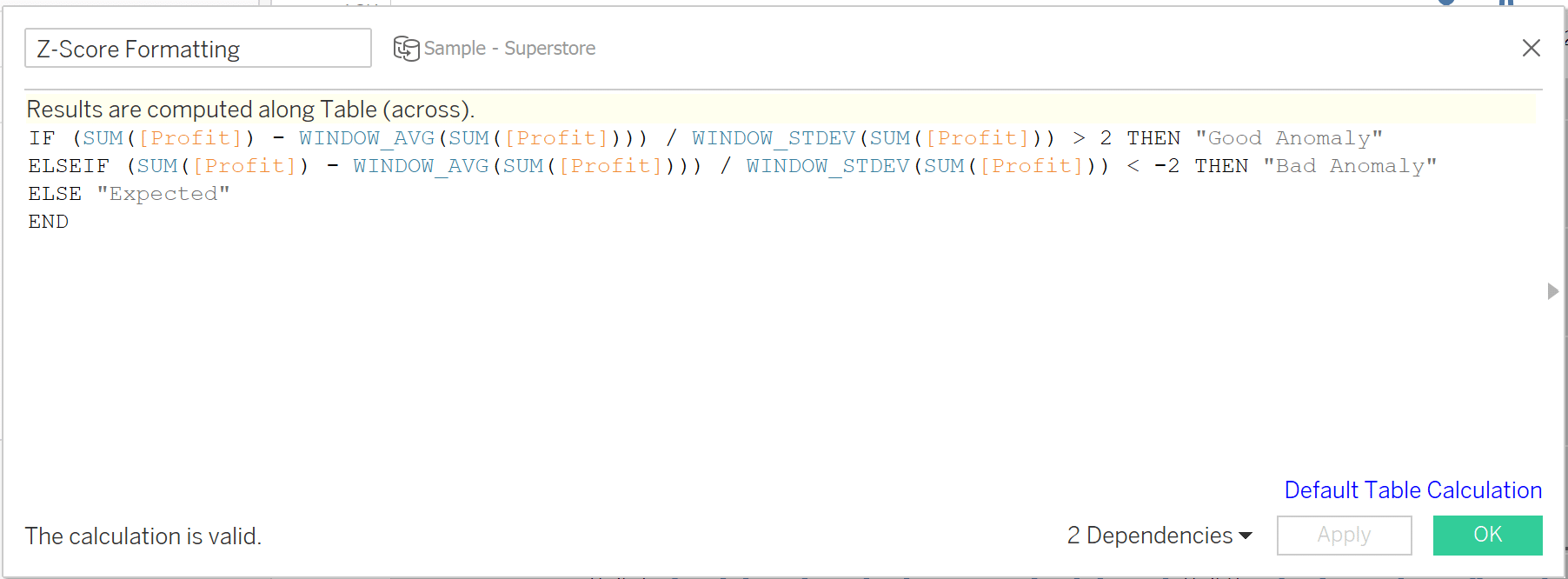
My view is starting to come together. Next, I’ll format the band fill, remove the text labels, and add some conditional formatting that will highlight my outliers. The formula for the conditional formatting is the following:

IF (SUM([Profit]) – WINDOW_AVG(SUM([Profit]))) / WINDOW_STDEV(SUM([Profit])) > 2 THEN “Good Anomaly”
ELSEIF (SUM([Profit]) – WINDOW_AVG(SUM([Profit]))) / WINDOW_STDEV(SUM([Profit])) < -2 THEN “Bad Anomaly”
ELSE “Expected”
END

Here is where I landed with my new formatting.

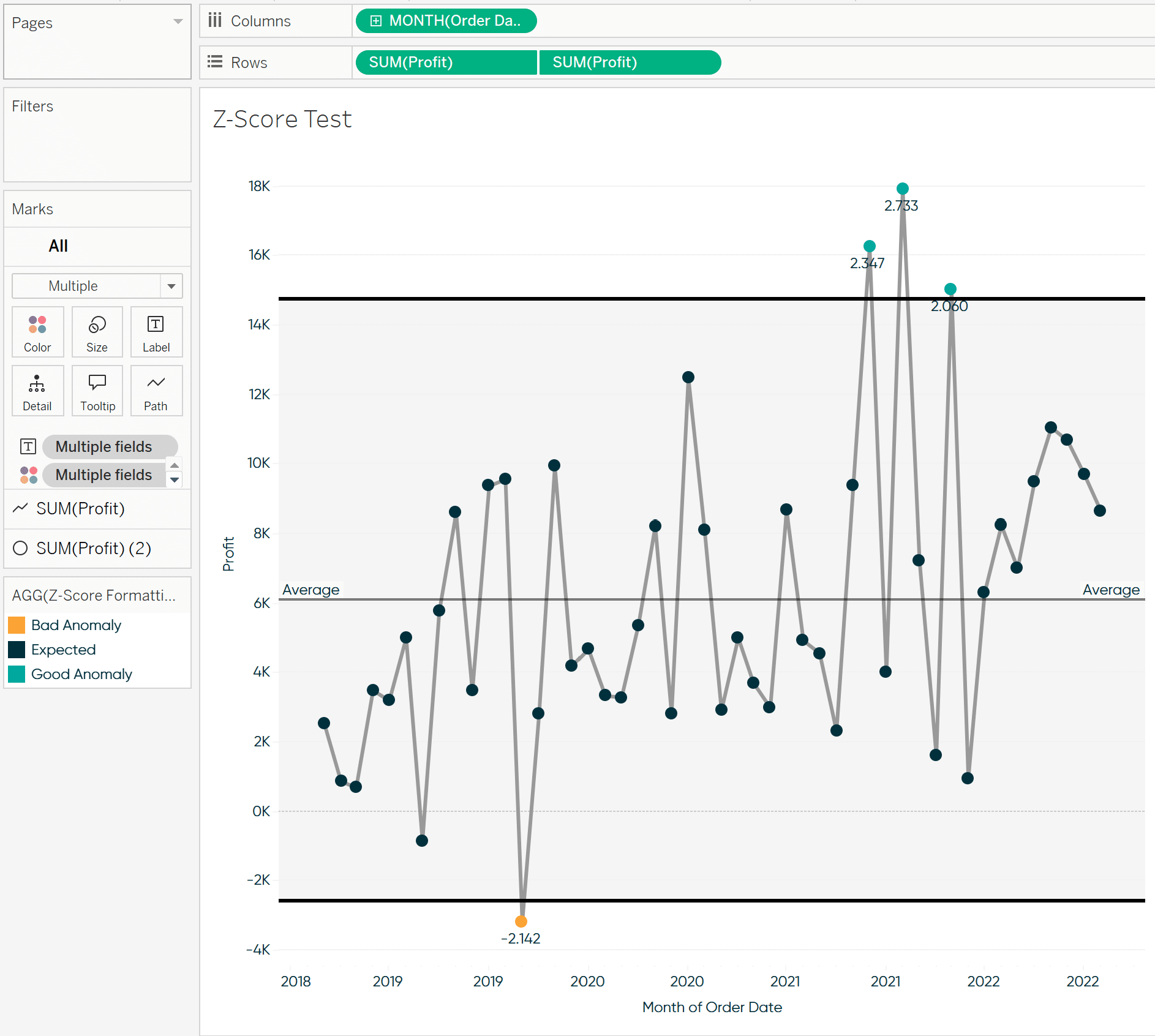
In closing, there are many methods out there to visualize outliers in your data. Each approach has its pros and cons, but my recommendation is to keep it as simple as possible and to visualize it.

Until Next Time,

Ethan Lang
Director, Analytics Engineering
[email protected]